Neo Sun


What's past is prologue

单变量线性回归

  • ~5.33K words
  1. 1. 监督式机器学习的基本术语
    1. 1.1. 标签和特征
    2. 1.2. 样本和模型
    3. 1.3. 训练
    4. 1.4. 损失
    5. 1.5. 定义损失函数
    6. 1.6. 训练模型的迭代方法
    7. 1.7. 模型训练要点
    8. 1.8. 收敛
    9. 1.9. 梯度下降法
    10. 1.10. 学习率
    11. 1.11. 超参数
  2. 2. 线性回归问题TensorFlow实战
    1. 2.1. 核心步骤
    2. 2.2. 人工数据集生成
    3. 2.3. 构建模型
    4. 2.4. 定义模型函数
    5. 2.5. 定义模型结构
    6. 2.6. 创建变量
    7. 2.7. 训练模型
    8. 2.8. 定义损失函数
    9. 2.9. 定义优化器
    10. 2.10. 创建会话
    11. 2.11. 迭代训练
    12. 2.12. 可视化
    13. 2.13. 最终可视化结果如下：
    14. 2.14. 小结
    15. 2.15. 完整程序附下：
  3. 3. 进阶
    1. 3.1. 显示损失值
    2. 3.2. 随机梯度下降

监督式机器学习的基本术语

标签和特征

标签是我们要预测的真实事物：y 线性回归中的y变量
特征是指用于描述数据的输入变量：xi 线性回归中的 {x1 ,x2 ,…,xn }变量

样本和模型

样本是指数据的特定实例：x
有标签样本具有{特征，标签}： {x ，y} //用于训练模型
无标签样本具有{特征，？}： {x ，?} //用于对新数据做出预测
模型可将样本映射到预测标签：y’ //由模型的内部参数定义，这些内部参数值是通过学习得到的

训练

训练模型表示通过有标签样本来学习（确定）所有权重和偏差的理想值

在监督式学习中，机器学习算法通过以下方式构建模型：
检查多个样本并尝试找出可最大限度地减少损失的模型
这一过程称为经验风险最小化

损失

损失是对糟糕预测的惩罚： 损失是一个数值，表示对于单个样本而言模型预测的准确程度
如果模型的预测完全准确，则损失为零，否则损失会较大
训练模型的目标是从所有样本中找到一组平均损失“较小”的权重和偏差

定义损失函数

L1损失 ：基于模型预测的值与标签的实际值之差的绝对值

平方损失 ：一种常见的损失函数，又称为 L2损失
均方误差 ( MSE) 指的是每个样本的平均平方损失

MSE

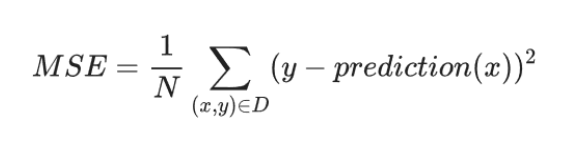
训练模型的迭代方法

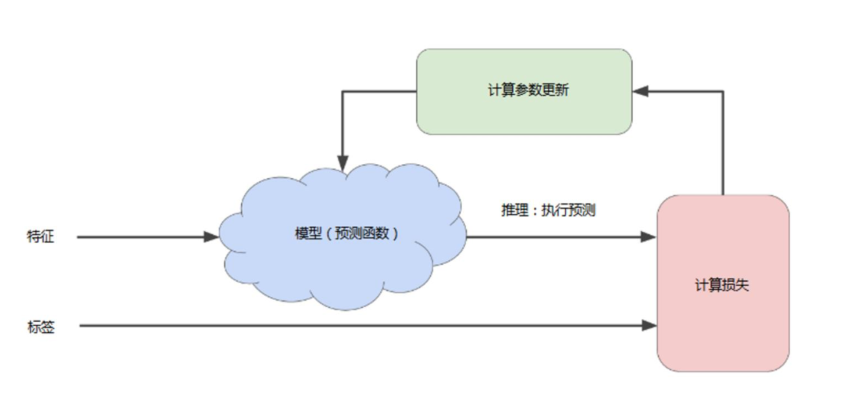
method

模型训练要点

首先对权重w和偏差b进行初始猜测，然后反复调整这些猜测，直到获得损失可能最低的权重和偏差为止

收敛

在学习优化过程中，机器学习系统将根据所有标签去重新评估所有特征，为损失函数生成一个新值，而该值又产生新的参数值。
通常，您可以不断迭代，直到总体损失不再变化或至少变化极其缓慢为止。这时候，我们可以说该模型已收敛

梯度下降法

梯度：一个向量（矢量），表示某一函数在该点处的方向导数沿着该方向取得最大值，即函数在该点处沿着该方向（此梯度的方向）变化最快，变化率最大

梯度是矢量:具有方向和大小

学习率

用梯度乘以一个称为学习速率（有时也称为 步长）的标量，以确定下一个点的位置

超参数

在机器学习中，超参数是在开始学习过程 之前设置值的参数，而不是通过训练得到的参数数据

通常情况下，需要对超参数进行优化，选择一组好的超参数，可以提高学习的性能和效果

超参数是编程人员在机器学习算法中用于调整的旋钮

典型超参数：学习率、神经网络的隐含层数量……

线性回归问题TensorFlow实战

核心步骤

（1）准备数据
（2）构建模型
（3）训练模型
（4）进行预测

人工数据集生成

1
2
3
4
5
6
7
8
9
10
11
12
13
14
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

np.random.seed(5)

x_data = np.linspace(-1,1,100)

y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4

plt.scatter(x_data,y_data)
plt.plot(x_data,2 * x_data +1.0,color = 'red',linewidth=3)

（可以使用tab键进行代码补齐）

构建模型

定位训练数据的占位符，x是特征值，y是标签值

1
2
x = tf.placeholder("float",name = "x")
y = tf.placeholder("float",name = "y")

定义模型函数

1
2
def model(x,w,b):
    return tf.multiply(x,w) + b

定义模型结构

创建变量

1
2
3
w = tf.Variable(1.0,name = "w0")
b = tf.Variable(0.0,name = "b0")
pred = model(x,w,b)

训练模型

设置训练参数

1
2
train_epochs = 10
learning_rate = 0.05

定义损失函数

• 损失函数用于描述预测值与真实值之间的误差，从而指导模型收敛方向
• 常见损失函数：均方差（Mean Square Error, MSE）和交叉熵（cross-entropy）

1
loss_function = tf.reduce_mean(tf.square(y-pred))

定义优化器

定义优化器Optimizer，初始化一个GradientDescentOptimizer
设置学习率和优化目标：最小化损失

1
2
3

optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

创建会话

声明会话
变量初始化

1
2
3
sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

迭代训练

模型训练阶段，设置迭代轮次，每次通过将样本逐个输入模型，进行梯度下降优化操作每轮迭代后，绘制出模型曲线

1
2
3
4
5
6
for epoch in range(train_epochs):
    for xs,ys in zip(x_data,y_data):
        _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    b0temp = b.eval(session = sess)
    w0temp = w.eval(session=sess)
    plt.plot(x_data,w0temp * x_data + b0temp)

可视化

1
2
3
4
plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data * sess.run(w) + sess.run(b),\
        label='Fitted line',color = 'r',linewidth=3)
plt.legend(loc=2)

最终可视化结果如下：

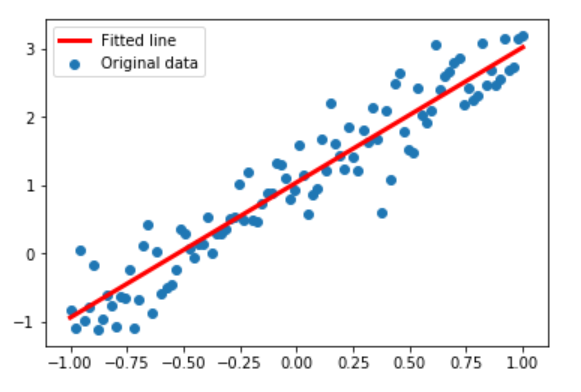
result

利用模型 进行预测

1
2
3
4
5
6
7
x_test = 3.21

predict = sess.run(pred, feed_dict={x: x_test})
print("预测值：%f"%predict)

target = 2 * x_test +1.0
print("目标值：%f"%target)

结果显示，模型预测结果极佳

小结

通过一个简单的例子介绍了利用Tensorflow实现机器学习的思路，重点讲解了下述步骤：
（1）生成人工数据集及其可视化
（2）构建线性模型
（3）定义损失函数
（4）定义优化器、最小化损失函数
（5）训练结果的可视化
（6）利用学习到的模型进行预测

完整程序附下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf

np.random.seed(5)

x_data = np.linspace(-1,1,100)

y_data = 2 * x_data + 1.0 + np.random.randn(*x_data.shape) * 0.4

x = tf.placeholder("float",name = "x")
y = tf.placeholder("float",name = "y")

def model(x,w,b):
    return tf.multiply(x,w) + b

w = tf.Variable(1.0,name = "w0")
b = tf.Variable(0.0,name = "b0")

pred = model(x,w,b)

train_epochs = 10
learning_rate = 0.05

loss_function = tf.reduce_mean(tf.square(y-pred))

optimizer = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss_function)

sess = tf.Session()
init = tf.global_variables_initializer()
sess.run(init)

for epoch in range(train_epochs):
    for xs,ys in zip(x_data,y_data):
        _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    b0temp = b.eval(session = sess)
    w0temp = w.eval(session=sess)
#    plt.plot(x_data,w0temp * x_data + b0temp)
    
plt.scatter(x_data,y_data,label='Original data')
plt.plot(x_data,x_data * sess.run(w) + sess.run(b),\
        label='Fitted line',color = 'r',linewidth=3)
plt.legend(loc=2)

x_test = 3.21

predict = sess.run(pred, feed_dict={x: x_test})
print("预测值：%f"%predict)

target = 2 * x_test +1.0
print("目标值：%f"%target)

进阶

显示损失值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
step = 0
loss_list = []
display_step = 10

for epoch in range(train_epochs):
    for xs,ys in zip(x_data,y_data):
        _,loss = sess.run([optimizer,loss_function],feed_dict={x:xs,y:ys})
    
        loss_list.append(loss)
        step=step+1
        if step % display_step == 0:
            print("Train Epoch:", '%02d'%(epoch+1),"Step:%03d"%(step),"loss=",\
                 "{:.9f}",format(loss))
    b0temp = b.eval(session = sess)
    w0temp = w.eval(session=sess)
    plt.plot(x_data,w0temp * x_data + b0temp)

随机梯度下降

在梯度下降法中， 批量指的是用于在单次迭代中计算梯度的样本总数

假定批量是指整个数据集，数据集通常包含很大样本（数万甚至数千亿），此外， 数据集通常包含多个特征。因此，一个批量可能相当巨大。如果是超大批量，则单次迭代就可能要花费很长时间进行计算

随机梯度下降法 ( SGD) 每次迭代只使用一个样本（批量大小为 1），如果进行足够的迭代，SGD 也可以发挥作用。“随机”这一术语表示构成各个批量的一个样本都是随机选择的

小批量随机梯度下降法（量 小批量 SGD）是介于全批量迭代与 SGD 之间的折衷方案。小批量通常包含 10-1000 个随机选择的样本。小批量 SGD 可以减少 SGD 中的杂乱样本数量，但仍然比全批量更高效

This work is licensed under Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)