数模竞赛基础

2022-03-22
Author 孙新斌
~15.69K words

1. （未完待续）

（未完待续）

对于今年的数学建模比赛的编程工作的准备与提高，按照本学期数模课程的进度更新，仅作为复习使用，持续更新

第一章数组运算与数组化编程

第一节数组的创建

matlab中的运算和操作主要是以数组（Array）为对象的，数组又包括：数值数组、字符数组、元胞数组等。

一、数值数组的建立：

1. 直接输入法

2.通过数组编辑器生成矩阵

3. 数据导入法

4.用函数创建数组

二、字符数组、元胞数组的建立

第二节数组的操作

1. 数组元素与子数组的提取

2.改变数组中的元素值与数组的拼接

——改变数组形状的命令

——数组的复制

3.常用的数组操作命令

——确定数组大小的命令

——排序命令

——稀疏矩阵与满矩阵的转化

——diag命令

——find命令

——排列组合

4.数组的运算

例题：

A=[4 3 2 5;
    3 4 3 2;
    2 3 4 3;
    5 2 3 4];
b = [1;-1;-2;3];
%(1)求A的逆矩阵
answer=A^-1
%(2)解方程组Ax=b
x = inv(A)*b
%(3)求A的特征值与特征向量
[V,D]=eig(A)

%输出
answer =

   -0.1579    0.1842   -0.3158    0.3421
    0.1842    0.3684   -0.1316   -0.3158
   -0.3158   -0.1316    0.3684    0.1842
    0.3421   -0.3158    0.1842   -0.1579


x =

    1.3158
   -0.8684
   -0.3684
   -0.1842


V =

    0.6533    0.2706    0.4483    0.5468
   -0.2706    0.6533   -0.5468    0.4483
    0.2706   -0.6533   -0.5468    0.4483
   -0.6533   -0.2706    0.4483    0.5468


D =

   -1.4142         0         0         0
         0    1.4142         0         0
         0         0    2.9010         0
         0         0         0   13.0990

第二章 MATLAB 图形功能

第一节曲线作图

一，曲线作图与图形控制

1.plot函数

2.图形窗口的控制

二，子图与多重线

1.子图

2.多重线

三，数字函数的简易作图

四，极坐标作图

第二节空间曲线和曲面作图

一，空间曲线作图

二，曲面作图

三，等高线图

例题：

%(1)
clear,clc;
close all;
x = -2:0.1:2;
y = -2:0.1:2;
[x,y]=meshgrid(x,y);
z = x.^2 + y.^2;
surf(x,y,z);
%(2)
[r,t]=meshgrid(0:0.1:2,0:0.02:2*pi);
x=r.*cos(t);
y=r.*sin(t);
z=x.^2+y.^2;
mesh(x,y,z)

(1)

(2)

第三章 Matlab程序设计

第一节自定义函数

一，符号函数

二，句柄函数

三，m-文件函数（子程序）

第二节流程控制语句

一，分支结构

——if语句

——switch语句

二，循环结构

——for循环语句

——while-end循环语句

三，程序的流程控制命令

A = randi([0,9],20,15)
result1 = 0;
result2 = 0;
for i=1:20
    for j=1:15
        if mod(A(i,j),5)==1
            result1 = result1 + A(i,j);
        elseif mod(A(i,j),5)==4
            result2 = result2 + A(i,j);
        end
    end
end
result1
result2

%结果
A =

  列 1 至 8

     4     2     9     9     3     3     1     9
     4     8     6     5     4     5     6     1
     5     8     2     5     6     5     8     2
     2     5     6     1     8     3     9     8
     7     8     0     8     6     3     5     5
     5     9     4     4     5     5     9     5
     6     5     6     2     3     6     5     6
     3     7     9     8     4     9     5     8
     1     5     8     7     7     7     3     5
     4     0     4     8     8     4     4     2
     3     4     7     2     7     8     4     4
     7     6     4     6     0     1     0     4
     7     5     9     6     6     0     8     9
     6     3     9     1     4     0     0     6
     1     9     8     4     4     1     4     6
     0     8     3     2     1     3     8     7
     5     8     4     7     8     3     3     3
     3     3     2     2     3     0     6     5
     9     5     7     8     2     5     8     5
     9     8     8     8     3     0     8     1

  列 9 至 15

     5     2     8     5     4     2     4
     6     8     0     1     8     0     9
     4     0     9     9     4     1     7
     8     8     1     5     3     1     0
     7     0     5     4     3     2     6
     3     6     1     9     1     1     7
     4     5     5     6     2     1     6
     3     2     0     4     0     5     5
     7     5     7     8     4     9     2
     7     1     8     5     2     9     7
     4     6     9     5     2     2     2
     6     5     9     6     4     4     3
     9     0     5     3     1     3     8
     7     0     2     2     4     5     8
     7     1     1     5     7     2     4
     1     0     5     8     2     0     3
     3     4     5     4     7     4     6
     5     8     7     1     0     1     9
     4     6     0     4     3     0     9
     0     5     6     3     0     9     5


result1 =

   193


result2 =

   386

第四章 Matlab数值运算

第三节数据插值

一，一维插值

——拉格朗日插值法

——分段插值

——三次样条插值

（1）yq=interp1(x,y,xq,’spline’)

（2）使用spline函数：

用法1：yq=spline(x, y, xq)

用法2：pp=spline(x, y)

获得三次样条插值的分段多项式pp，

可使用ppval计算插值。

（3）使用csape函数：

用法： pp=csape(x, y)

可以添加参数选择边界条件。

二，二维插值

1.网格节点数据插值函数：interp2

2.散点数据插值函数：griddata

%曲线拟合
clf
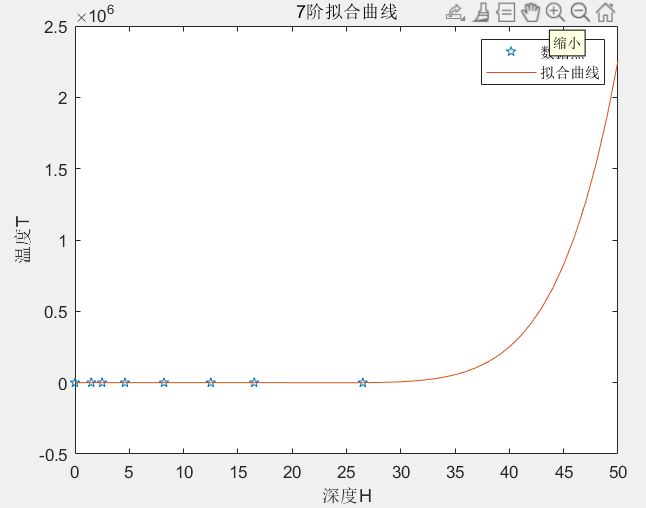
t = [23.5 22.9 20.1 19.1 15.4 11.5 9.5 8.2];
h = [0 1.5 2.5 4.6 8.2 12.5 16.5 26.5];
plot(h,t,'p')
hold on
y = polyfit(h,t,7);
tem = poly2str(y,'H')
h = 0:1:50;
y1 = polyval(y,h);
plot(h,y1)
xlabel('深度H'),ylabel('温度T')
legend('数据点','拟合曲线')
title('7阶拟合曲线')
%最值求取
syms H
T = 1.674e-05*H^7 - 0.0011747*H^6 + 0.030973*H^5 - 0.38897*H^4 + 2.4095*H^3
        - 6.7843*H^2 + 5.5198*H + 23.5
dT = diff(T,H)
dT2 = diff(T,H,2)
Tj = solve(dT2,H)
Tj1 = subs(dT,'H',Tj)

%结果：
tem =
    '   1.674e-05 H^7 - 0.0011747 H^6 + 0.030973 H^5 - 0.38897 H^4 + 2.4095 H^3- 6.7843 H^2 + 5.5198 H + 23.5'

 
dT =
(17292715764458281*H^6)/147573952589676412928 - (16252042697539959*H^5)/2305843009213693952 + (5579599650341855*H^4)/36028797018963968 - (38897*H^3)/25000 + (14457*H^2)/2000 - (67843*H)/5000 + 27599/5000
 
 
dT2 =
(51878147293374843*H^5)/73786976294838206464 - (81260213487699795*H^4)/2305843009213693952 + (5579599650341855*H^3)/9007199254740992 - (116691*H^2)/25000 + (14457*H)/1000 - 67843/5000
 
 
Tj =
 root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)
 root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)
 root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)
 root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)
 root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)
 
 
Tj1 =
 (14457*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)^2)/2000 - (38897*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)^3)/25000 + (5579599650341855*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)^4)/36028797018963968 - (16252042697539959*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)^5)/2305843009213693952 + (17292715764458281*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1)^6)/147573952589676412928 - (67843*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 1))/5000 + 27599/5000
 (14457*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)^2)/2000 - (38897*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)^3)/25000 + (5579599650341855*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)^4)/36028797018963968 - (16252042697539959*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)^5)/2305843009213693952 + (17292715764458281*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2)^6)/147573952589676412928 - (67843*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 2))/5000 + 27599/5000
 (14457*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)^2)/2000 - (38897*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)^3)/25000 + (5579599650341855*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)^4)/36028797018963968 - (16252042697539959*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)^5)/2305843009213693952 + (17292715764458281*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3)^6)/147573952589676412928 - (67843*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 3))/5000 + 27599/5000
 (14457*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)^2)/2000 - (38897*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)^3)/25000 + (5579599650341855*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)^4)/36028797018963968 - (16252042697539959*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)^5)/2305843009213693952 + (17292715764458281*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4)^6)/147573952589676412928 - (67843*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 4))/5000 + 27599/5000
 (14457*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)^2)/2000 - (38897*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)^3)/25000 + (5579599650341855*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)^4)/36028797018963968 - (16252042697539959*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)^5)/2305843009213693952 + (17292715764458281*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5)^6)/147573952589676412928 - (67843*root(z^5 - (866775610535464480*z^4)/17292715764458281 + (45708080335600476160*z^3)/51878147293374843 - (358761502117540214603776*z^2)/54039736763932128125 + (44447429845603164618752*z)/2161589470557285125 - 625741229096338555142144/32423842058359276875, z, 5))/5000 + 27599/5000

第四节数值积分

一，数值积分的常用方法

（1）用梯形法计算积分

（2）一维数值积分

二，重积分的数值计算

（1）数值二重积分

（2）数值三重积分

例题

function dy=rigid(t,y)
       dy=zeros(3,1);
       dy(1)=y(2)*y(3);
       dy(2)=-y(1)*y(3);
       dy(3)=-0.51*y(1)*y(2);
end

[T,Y]=ode45('rigid',[0 12],[0 1 1]);
plot(T,Y(:,1),'-',T,Y(:,2),'.',T,Y(:,3),'+')

Neo Sun

数模竞赛基础

（未完待续）

第一章数组运算与数组化编程

第一节数组的创建

第二节数组的操作

第二章 MATLAB 图形功能

第一节曲线作图

第二节空间曲线和曲面作图

第三章 Matlab程序设计

第一节自定义函数

第二节流程控制语句

第四章 Matlab数值运算

第三节数据插值

第四节数值积分

This work is licensed under Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)

Neo Sun

（未完待续）

第一章 数组运算与数组化编程

第一节 数组的创建

第二节 数组的操作

第二章 MATLAB 图形功能

第一节 曲线作图

第二节 空间曲线和曲面作图

第三章 Matlab程序设计

第一节 自定义函数

第二节 流程控制语句

第四章 Matlab数值运算

第三节 数据插值

第四节 数值积分

This work is licensed under Attribution-ShareAlike 4.0 International (CC BY-SA 4.0)

第一章数组运算与数组化编程

第一节数组的创建

第二节数组的操作

第一节曲线作图

第二节空间曲线和曲面作图

第一节自定义函数

第二节流程控制语句

第三节数据插值

第四节数值积分