第一章

能判断它是一个P,NP问题（涉及复杂度）

时间的上界和下界（最好、最坏情况）（通项）

一、递推方法求递归算法的时间复杂性

二、Master定理方法求递归算法时间复杂性

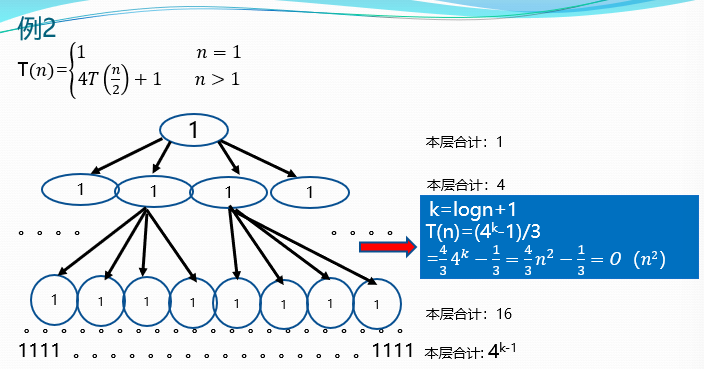
三、递归树求解递归方程

P、NP问题

NP完全性理论

多项式与非多项式时间复杂性

易解的：可在多项式时间内求解

难解的：不可在多项式时间求解

P问题：确定的算法+多项式时间求解+可判定问题（多项式类型）

NP问题：不确定的算法+多项式时间求解+可判定问题

NPC问题：NP问题+多项式归约为D

意义：有一个NPC问题找到多项式时间的解法，则全部解决

第二章 递归与分治

循环赛日程表

棋盘覆盖问题

平衡(balancing)子问题的思想：将一个问题分成大致相等的k个子问题，算法最有效。

分治法所能解决的问题一股具有以下四个特征：
●该问题的规模缩小到一定的程度就可以容易地解决。（能分）
●该问题可以分解为若干个规模较小的相同问题。（规模小）
●使用小规模的解可以合并成，该问题原规模的解。（能合）
●该问题所分解出的各个子规模是相互独立的。（无重复子问题）

1
2
3
4
5
6
7
8
9
10
11

//归并排序
void MergeSort(Type a[], int left, int right)
   {
      if (left<right) {//至少有2个元素
     	 int i=(left+right)/2;  //取中点
     	 mergeSort(a, left, i);
      	 mergeSort(a, i+1, right);
    	 merge(a, b, left, i, right);  //合并到数组b
      	 copy(a, b, left, right);    //复制回数组a
      }
   }

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

//快速排序（partition）
template<class Type>
void QuickSort (Type a[], int p, int r)
{
      if (p<r) {                                                  
        int q=Partition(a,p,r);
        QuickSort (a,p,q-1); //对左半段排序
        QuickSort (a,q+1,r); //对右半段排序
        }
}
int Partition (int a[], int p, int r)
{	int i = p, j = r + 1;
	int t;
	int x=a[p];    //a[p]做划分基准
	//  将数据分为二部分：左边的元素<=x, 右边的元素>x，x放中间。
	while(1)
	{   while (a[++i] <=x && i<r) ; //从左向右找>x的数的位置下标i,找不到时i==r
	    while (a[--j] >x) ;            //从右向左找<=x的数的位置下标j,找不到时j==p
	    if (i>=j) break;             //一遍扫描结束， 退出循环
	    t=a[i];
	    a[i]=a[j];
	    a[j]=t;
	}
	a[p] = a[j];  //首元素a[p]与a[j] 交换
	a[j] = x;       //x放在分界点
	return j;      //j是分裂位置
}

1
2
3
4
5
6
7
8
9
10
11

//分治法算法框架
Type abc(参数)
｛
   if（满足边界条件）
       ……；
   else
    ｛
      	……；
   	……；
     ｝
｝

第三章 动态规划

动态规划的基本要素：

1. 最优子结构性质
2. 重叠子问题性质

备忘录方法

分治与动态规划的联系和区别：

分治可使用递归和非递归方法，因为没有任何两个子问题是重复的， 所以没有多余的计算量。

动态规划采用自底向上的方法求解问题，每次求解的问题都是不同的

因为是自底向上的方式， 所以在求解一个大问题时，比他规模小的问题的答案已经存在了， 可以直接通过这些小问题的答案去合并为大问题答案即可

动态规划算法会产生至少一张表，就是用来记录答案的，还有一张表（辅助构造最优解的辅助表）不是必须的，有时候直接可通过第一张表就可构造出最优解。

动态规划最后求解的问题是规模最大的问题，也就是我们需要解决的问题

矩阵连乘问题（最大子段和问题）

凸多边形三角剖分

游艇问题

0-1背包问题（优先队列）

数字塔问题：计算最优解

第四章 贪心算法

证明最优子结构和贪心选择性质

背包问题

哈夫曼树的贪心策略，构造编码树

贪心策略：

每次选择两个最低发生频率的结点构造一颗子树的根结点。并把产生的子树的根结点再插入到优先队列中

（按结点的频率值组织为最小优先队列）

贪心选择的基本要素：

1. 贪心选择性质

   贪心选择性质：是指所求问题的整体最优解，可以通过一系列局部最优的选择，即贪心选择来达到。

   贪心选择性质证明方法：一步步的贪心选择（局部最优）最终导致问题的整体最优解。

2. 最优子结构性质

   当一个问题的最优解包含其子问题的最优解时，称此问题具有最优子结构性质。

   因为最优解对应最优值，所以通常证明：问题的最优值包含其子问题的最优值。

贪心算法与动态规划算法的差异

性质相同点：贪心算法和动态规划算法都要求问题具有最优子结构性质

性质不同点：贪心算法要求问题具有贪心选择性质，动态规划算法则不要求。

计算方式的不同：

动态规划算法通常以自底向上的方式解各子问题

贪心算法以自顶往下的方式进行，每做一次贪心选择就将问题变为规模更小的子问题。

最优装载问题的证明：

贪心选择性质

设集装箱依其重量从小到大排序，（x1,x2,..xn)是其最优解，xi={0,1}，设xk是第一个等于1的。

（1）如k=1， 则满足贪心选择性质

（2）如k≠1，用x1替换xk，构造的新解同原解最优值相同，故也是最优解，满足贪心选择性质。

最优子结构性质

最优装载问题具有最优子结构性质. 设1至n个集装箱装上船的最大数量为T(1,n,w）

则 T(1,n,w)=1+T(2,n,w-w1) ；

因T(1,n,w)是最优值，则T(2,n,w-w1)一定是最优值。反证法证明之。

反证法

如果T(2,n,w-w1)不是该问题的最优值，则存在最优值 T ‘(2,n,w-w1)> T(2,n,w-w1)，则 1+ T ‘(2,n,w-w1) = T ‘(1,n,w)> T(1,n,w),这与大前提T(1,n,w)是最优值相矛盾， 故T(2,n,w-w1)一定是最优值

第五章 回溯法

子集树、排列树

构造解空间

符号三角形问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

void backtrack (int t)
   {   if ((count>half)||(t*(t-1)/2-count>half)) return;
       if (t>n) sum++;
       else
           for (int i=0;i<2;i++) {    //(+ as 0，- as 1）
          	 p[1][t]=i;
          	 count+=i;
          	 for (int j=2;j<=t;j++) {
                    p[j][t-j+1]=p[j-1][t-j+1]^p[j-1][t-j+2];
                     count+=p[j][t-j+1]; }
              backtrack(t+1);
              for (int j=2;j<=t;j++)  count-=p[j][t-j+1];
              count-=i;
           }
   }

n皇后问题（排列树）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

bool Queen:Place(int k)
{
  for (int j=1;j<k;j++)
    if (abs(k-j)==abs(x[j]-x[k])) 
           return false;
  return true;
} 
void Queen::Backtrack(int t)
{
  if (t>n) sum++;
    else
      for (int i=t;i<=n;i++) {
         swap(x[t],x[i]);
         if (Place(t))   	Backtrack(t+1);
         swap(x[t],x[i]);
      }
 }

0-1背包问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

void Backtrack(int i)
{if (i>n) {//到达叶节点
    bestp=cp；    return；}
If（cw+w[i]<=c){进入左子树
    	cw+=w[i];
	cp+=p[i];
	Backtrack(i+1);
	cw-=w[i];
	cp-=p[i];}
 If(Bound(i+1)>bestp)
    Backtrack(i+1);
}
template<class Typew, class Typep>
Typep Knap<Typew, Typep>::Bound(int i)
{// 计算上界
   Typew cleft = c - cw;  // 剩余容量, cw当前在背包中物品重量
   Typep b = cp; 	  //cp当前在背包中物品价值
   // 以物品单位重量价值递减序装入物品
   while (i <= n && w[i] <= cleft) {
      cleft -= w[i];
      b += p[i];
      i++;
      }
   // 装满背包
   if (i <= n) b += p[i]/w[i] * cleft;
   return b;
}

最大团问题

•解空间：子集树

•可行性约束函数：顶点i到已选入的顶点集中每一个顶点都有边相连。

•上界函数:有足够多的可选择顶点使得算法有可能在右子树中找到更大的团。

着色问题

•解向量：(x1, x2, … , xn)表示顶点i所着颜色xi

•可行性约束函数：顶点i与已着色的相邻顶点颜色不重复。

圆排列问题

去镜像排列：1,2,3和3,2,1这种互为镜像的排列具有相同的圆排列长度，只计算一个就够了，可减少约一半的计算量。

方法：保证每个排列的首元素一定小于尾元素即可，排列的元素在本题中是圆的半径

剪枝、可行性约束、限界

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//装载问题
void backtrack (int i)
   {// 搜索第i层结点
      if (i > n)  // 到达叶结点
           更新最优解bestx,bestw;return;
  if (cw + w[i] <= c) {// 搜索左子树
         r - = w[i];
         x[i] = 1; 
         cw += w[i];
         backtrack(i + 1); 
         cw -= w[i];
         r += w[i]; }
 if (cw + r-w[i] > bestw)  {// 搜索右子树
	r - = w[i]; 
	x[i] = 0; 
        backtrack(i + 1); 
        r += w[i]; } 
 }

用回溯法解装载问题的时间复杂性是O(2^n^)。

第六章 分支限界法

回溯法与分支限界法的区别

（1）求解目标：

回溯法求解目标是找出解空间树中满足约束条件所有解

分支限界法的求解目标则是找出满足约束条件的一个解（或一个最优解）

（2）搜索方式的不同：

回溯法以深度优先方式搜索解空间树

分支限界法则以广度优先或以最小耗费优先方式搜索解空间树

队列与优先队列的区别

1. 队列式：活结点表是一个队列，新扩展出的满足条件的活结点追加在队尾。这里需要加入层次标志（如-1），或记录下层编号在活结点中。

2. 优先队列式：活结点表是优先队列，一般使用堆（大顶堆或小顶堆）存储，优点是只需要O（logn）时间复杂性完成插入或者删除（取堆顶结点，即优先级最高的结点）

3. 构造解方法， 活结点通过记录其父节点地址，及左孩子标志去，在找到最优值时，回溯方法找到最优解。也可在扩展出的结点中记录构造的解，如问题规模较大时，应考虑压缩存储。

4. 分支限界法的剪枝方法：

   （1）对于子集树，左右分支剪枝策略不同，

   （2）对于排列树，n叉树， 剪枝策略是相同的。

5. 算法的结束控制：

   （1）队列式分支限界， 活结点表为空

   （2）优先队列式，叶子结点成为扩展结点(在确认后面的活结点不存在更好的解)或队列为空。通常叶子结点加入优先队列中。

装载问题

最优解构造

布线问题

0-1背包问题

第七章 概率算法

数值随机化算法常用于数值问题的求解，得到的往往是近似解，且近似解的精度随计算时间的增加而不断提高。

蒙特卡罗算法(Monte Carlo)用于求问题的准确解。但这个解未必是正确的。其求得正确解的概率依赖于算法所用的时间，算法所用的时间越多，得到正确解的概率就越高。缺点：一般情况下，无法有效地判断得到的解是否肯定正确。（1主元素问题、素数问题、）

重复调用一个一致的、p正确的、偏y~0~蒙特卡罗算法k次，可得到一个1-(1-p)^k^正确的蒙特卡罗算法，且所得算法仍是一个一致的偏y~0~蒙特卡罗算法。

换句话说：如果蒙特卡洛对同一个实例，连续运行k次， 答案都是一样的， 则这个答案正确的可能性是 1-(1-p)^k^。

如k足够大，则该答案的正确性就足够高

设p是一个实数，且1/2<p<1。如果一个蒙特卡罗算法对于问题的任一实例得到正确解的概率不小于 p，则称该蒙特卡罗算法是p正确的，且称p-1/2是该算法的优势。

如果对于同一实例，蒙特卡罗算法不会给出2个不同的正确解答，则称该蒙特卡罗算法是一致的。
对于一个解所给问题的蒙特卡罗算法MC(x)，如果存在问题实例的子集X使得：
(1)当x不属于X时，MC(x)返回的解总是正确的；
(2)当x∈X时，正确解是y0，但MC(x)返回解未必是y0。称MC(x)是偏y0的算法。

拉斯维加斯算法(Las Vegas)不会得到不正确的解。但有时找不到解。（n皇后）

舍伍德算法(Sherwood)总能求得问题的一个解，且求得的解总是正确的。精髓：不是避免算法的最坏情形行为，而是设法消除这种最坏情形与特定实例之间的关联性。（线性时间选择算法、快速排序算法、跳跃表）