01 绪论
02 自动推理
1.概述
确定性推理与不确定性推理
- 按推理时所用知识的确定性来划分,推理可分为确定性推理、不确定性推理
- 确定性推理:推理时所用的知识都是精确的,推出的结论也是确定的,其真值或者为真,或为假,没有第三种情况出现
- 不确定性推理:推理时所用的知识不都是精确的,推出的结论也不完全是肯定的,真值位于真与假之间,命题的外延模糊不清
启发式推理与非启发式推理
- 按推理过程中是否运用启发式知识分类:
- 启发式推理:在推理过程中运用了与问题有关启发式知识,即解决问题的策略、技巧和经验,加快了推理过程,提高了搜索效率。
- 非启发式推理:在推理过程中只按照一般的控制逻辑进行推理。缺乏对求解问题的针对性,推理效率较低,容易出现组合爆炸问题。
搜索策略
- 盲目搜索:也称为无信息搜索,即只按预定的控制策略进行搜索,在搜索过程中获得的中间信息不用来改进控制策略。
- 启发式搜索: 在搜索中加入了与问题有关的启发性信息,用于指导搜索朝着最有希望的方向进行,加速问题的求解过程并找到最优解。
2.启发式搜索
前面讨论的方法都是盲目的搜索方法,即都没有利用问题本身的特性信息,在决定要被扩展的节点时,都没有考虑该节点在解的路径上的可能性有多大,它是否有利于问题求解以及求出的解是否为最优
启发信息的强度
- 强:降低搜索工作量,但可能导致找不到最优解
- 弱:一般导致工作量加大,极限情况下变为盲目搜索,但可能可以找到最优解
启发性信息和估价函数
用于指导搜索过程,且与具体问题有关的控制性信息称为为启发性信息
用于评价节点重要性的函数称为估价函数.记为
- g(x)为从初始节点S~0~到节点x已经实际付出的代价
- h(x)是从节点x到目标节点S~g~的最优路径的估计代价,体现了问题的启发性信息,称为启发函数
- f(x)表示从初始节点经过节点x到达目标节点的最优路径的代价估价值,其作用是用来评估OPEN表中各节点的重要性,决定其次序。
爬山算法基本思想
利用评估函数f(x)来估计目标状态和当前状态的“距离”。
①当一个节点被扩展后,对子节点x进行评估得到f(x),按f(x)的升序排列并把这些节点压人栈。因此,栈顶元素具有最小的f(x)值。
②弹出栈顶元素并和目标状态比较。如果栈顶元素不是目标,则扩展栈顶元素,并计算其所有子状态的f值,并按升序把这些子状态压入栈中。
③如果栈顶元素是目标,则算法退出。否则该过程循环下去,直至栈为空。
最好优先算法:从最有希望的节点开始,并生成其所有的子女节点。然后计算所有节点的性能,基于该性能选择最有希望的节点扩展,而不仅仅是从当前节点所生成的子女节点中选择。
A*算法
启发式函数h(x)的选取、求解过程、画搜索图、open表与close表(详见 PPT)
启发性信息越强,搜索节点越少;启发性信息越弱,搜索节点越多;
3.与或图启发式搜索
在问题求解过程中,将一个大的问题变换成若干个子问题,子问题又可以分解成更小的子问题,这样一直分解到可以直接求解为止,全部子问题的解就是原问题的解。
与或图(详见PPT)
A*算法不能搜索与或图
4.博弈搜索$
博弈树
博弈树特点
博弈中两种最基本的搜索方法
MAXMIN基本思想
极大极小搜索过程
α-β搜索过程
α剪枝法
α-β剪枝的弱点
03 不确定性推理
主观贝叶斯有原题
什么是不确定性推理?
- 是从不确定性的初始证据出发,通过运用不确定性的知识,最终推出具有一定程度的不确定性但却合理或者近乎合理的结论的思维过程。
- 确定性是智能问题的本质特征,可以说智能主要反映在求解不确定性问题的能力上。
可信度方法$


主观贝叶斯$
经典概率方法部分(见PPT)








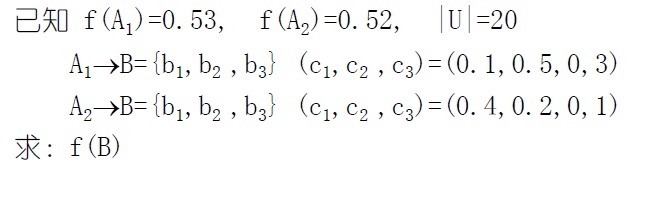
05-1 机器学习基础
机器学习方法分类
最常见的分类方式:
- 监督(supervised)学习: 根据已知类别的训练样本(known sample) ,由机器从其中进行学习或者训练,从中勾画出各类事物在特征空间分布的规律性,进而对新样本进行判断;
无监督(unsupervised)学习或聚类(clustering):由机器从未知类别的样本(unknown sample)中进行学习(自学习),从中发现有利于对象分类的规律;
半监督(semi‐supervised)学习:由机器利用部分已知类别的样本,从中恢复样本的相关附加信息,进而进行聚类分析。
机器学习中的几个关键数学问题
机器学习不同类型的问题
- 聚类 2. 分类 3. 强化学习 4.回归
从数学的角度看分类问题
已知:
(1)函数的值域为有限个离散点
(2)函数在某些点上的函数值。
回归问题与分类问题的关系
分类:
因此回归可以看成是分类问题的推广,可以看成是类别数为不可数时的分类问题。但我们不能以此简单地认为回归问题比分类问题难,事实上由于回归问题的值域为整个实数域,常常更好处理。
如何调整θ以使得J(θ)取得最小值有很多方法,其中有最小二乘法(min square)、梯度下降法、牛顿法。
最小二乘法的局限性
只有当矩阵A的每一列都是线性不相关的,矩阵A^T^ A才是可逆的。
- A^T^ A不可逆,无法求解
- 当特征维数大时,A^T^ A求逆困难
梯度下降法(Gradient Descent)
- 梯度即是某一点最大的方向导数,沿梯度方向函数有最大的变化率(正向增加,逆向减少)
- 代价函数J沿梯度的负方向下降最快
梯度下降法的关键因素
- 初值选择
- 步长α的选择
梯度下降法小结
梯度下降不一定能够找到全局的最优解,有可能是一个局部最优解。当然,如果损失函数是凸函数,梯度下降法得到的解就一定是全局最优解。
步长太大,会导致迭代过快,甚至有可能错过最优解 。步长太小,迭代速度太慢,很长时间算法都不能结束 。所以算法的步长需要多次运行后才能得到一个较为优的值。
逻辑回归(Logistics Regression)
解决分类问题
线性回归+阈值 缺点:健壮性不够,对噪声敏感
如使用线性回归,则可得到图中粉色的直线
确定一个threshold:0.5进行预测:
能够很好地进行分类
因此,引入逻辑回归模型来解决分类问题 。
Sigmod函数性质
逻辑回归(Logistics Regression)
05-3 线性分类器
05-4 非线性分类器
支持向量机,一种线性和非线性数据有前途的新划分类方法。巧妙利用向量内积的回旋,通过引入非线性核函数将问题变为高维特征空间与低维输入空间的相互转换,解决了数据挖掘中的维数灾难。由于计算问题最终转化为凸二次规划问题,因此挖掘算法是无解或有全局最优解。
※ 什么是支持向量(简单来说,就是支持或支撑平面上把两类类别划分开的向量点)
※ 这里的“机(machine,机器)”便是一个算法。在机器学习领域,常把一些算法看做是一个机器,如分类机(当然,也叫做分类器),而支持向量机本身便是一种监督式学习的方法,它广泛的应用于统计分类以及回归分析中。
目标:找到一个超平面,使得它能够尽可能多的将两类数据点正确的分开,同时使分开的两类数据点距离分类面最远。
最优分类超平面
支持向量
核方法
make linear model work in nonlinear settings!
目前研究最多的核函数主要有三类:
多项式内核
高斯径向基函数内核RBF
Sigmoid内核
SVM实现非线性分类的思想
Boosting算法
Adaboost分类器
- 弱分离器
- 强分类器
- Adaboost 训练算法
- 级联(cascade)分类器
提升方法(boosting)
分类器的实现—Adaboost算法
05-5 决策树
06-1 人工神经网络
概述
神经网络(neural networks, NN),也称作人工神经网络( artificial neural networks, ANN),或神经计算(neural computing, NC),是对人脑或生物神经网络的抽象和建模,具有从环境学习的能力,以类似生物的交互方式适应环境。
神经元是大脑的主要计算单元。
感知机
感知器的学习就是修改权值和偏置的过程。
感知器学习规则
感知器特别适合解决简单的模式分类问题。
单层感知器的局限性
XOR问题的解决——多层感知器网络
两层感知器结构
多层感知器神经网络的分类能力
多层感知器研究的瓶颈
人工神经网络发展
- 前馈神经网络:BP网络、RBF网络
- 反馈神经网络: 以Hopfield模型为代表
- 自组织网络(竞争学习网络): 以SOM模型为代表
- 深度神经网络:CNN、RNN
前馈神经网络
MLP网络特性
MLP网络特性:可以实现任意复杂的非线性映射关系用于分类:
- 两层网(一个隐层)可以实现空间内任意的凸区域的划分
- 三层网(两个隐层)可以实现任意形状(连续或不连续)区域的划分
BP算法
- 既然我们无法直接得到隐层的权值,能否先通过输出层得到输出结果和期望输出的误差来间接调整隐层的权值呢?
- 提出由Sigmoid函数代替之前的阶跃函数作为激励函数来构造神经元。
- Sigmoid函数是单调递增的非线性函数,函数本身及其导数都是连续的,无限次可微。
BP算法的基本思想
BP网络的拓扑结构
前馈神经网络的计算
反向传播(back-propagation,BP)
BP算法的改进
BP网络的特点
RBF神经网络基本结构
- 三层神经网络:输入层、输出层及一个隐层
- 隐层节点激活函数为径向基函数,输出节点激活函数为线性函数。
- 输入层与隐层无权连接,隐层与输出层是线性加权,即网络可调参数。
RBF与BP神经网络的区别
全局逼近 vs 局部逼近
BP网络对目标函数的逼近跟所有数据都相关
RBF网络对目标函数的逼近仅仅根据中心点附近的数据。
RBF神经网络与SVM的区别
RBF网络的应用
反馈神经网络:Hopfield网络
Hopfield网络是神经网络发展历史上的一个重要的里程碑。由美国加州理工学院物理学家J.J.Hopfield教授于1982年提出,是一种单层反馈神经网络。
Hopfield网络分为离散型和连续型两种网络模型,分别记作DHNN (Discrete Hopfield Neural Network) 和CHNN
(Continues Hopfield Neural Network) 。
06-2 BP算法推导
07-1 深度学习CNN
卷积神经网络的特点
可以当作是一个分类器,也可以看作是一种特征提取方式(把中间某一层的输出当作数据的一种特征表示)。
CNN能够得出原始图像的有效表征,这使得CNN能够直接从原始像素中,经过极少的预处理,识别视觉上面的规律。避免了传统识别算法中复杂的特征提取和数据重建过程。
- 基于大规模的数据。每个网络都有众多的参数,少量数据无法将参数训练充分。
- 卷积网络是为识别二维形状而特殊设计的一个多层感知器,这种网络结构对平移、比例缩放、倾斜或者共他形式的变形具有高度不变性。
卷积神经网络的核心思想
- 局部感知
- 权重共享
- 多卷积核
- 空间下采样
目标1:减少参数,降低复杂度
目标2:实现卷积特征自动提取
将局部感知、权值共享以及空间亚采样这三种结构思想结合起来获得了某种程度的位移、尺度、形变不变性。
由于一个映射面上的神经元共享权值,因而减少了网络自由参数的个数,降低了网络参数选择的复杂度。
卷积神经网络中的每一个特征提取层(C-层)都紧跟着一个用来求局部平均与二次提取的计算层(S-层),这种特有的两次特征提取结构使网络在识别时对输入样本有较高的畸变容忍能力。
如何确定隐层神经元的个数?
卷积神经网络核心思想四:空间下采样
卷积神经网络的基本结构
CNN网络 vs BP网络
实例:卷积神经网络实现手写数字识别: LeNet-5 $
上图模型的基本参数
输入:224×224大小的图片,3通道
第一层卷积:5×5大小的卷积核96个,每个GPU上48个。步长为4,得到卷积图为55*55.
第一层max-pooling:2×2的
核。
第二层卷积:3×3卷积核256个,每个GPU上128个。
第二层max-pooling:2×2的核。
第三层卷积:与上一层是全连接,3*3的卷积核384个。分到两个GPU上个192个。
模型参数
第四层卷积:3×3的卷积核384个,两个GPU各192个。该层与上一层连接没有经过pooling层。
第五层卷积:3×3的卷积核256个,两个GPU上各128个。
第五层max-pooling:2×2的核。
第一层全连接:4096维,将第五层max-pooling的输出连接成为一个一维向量,作为该层的输入。
第二层全连接:4096维
Softmax层:输出为1000,输出的每一维都是图片属于该类别的概率。
网络模型优化:梯度下降法
- 在处理复杂任务上,深度网络比浅层的网络具有更好的效果。
- 目前优化神经网络的方法都是基于误差反向传播的思想,即根据损失函数计算的误差通过梯度反向传播的方式,指导深度网络权值的更新优化。
- 优化目标:损失函数Loss求最小值。
- 寻找最小值问题:梯度下降法。
梯度发散 vs 梯度爆炸
梯度发散:sigmod函数
梯度发散:tanh函数
如何解决梯度消失及梯度爆炸?
ReLU激活函数
ReLU函数的主要贡献:
ReLU缺点:
梯度爆炸解决方案
Batch normalization(批规范化)
因此我们可以通过固定每一层网络输入值的分布来对减缓问题。
数据增强(data augmentation)
L2 regularization
Dropout
Dropout基本思路:
- 在开始,随机删除掉隐藏层一部分的神经元,如图,虚线部分为开始时随机删除的神经元:
- 然后,在删除后的剩下的神经元上正向和反向更新权重和偏向;
- 再恢复之前删除的神经元,再重新随机删除一半的神经元,进行正向和反向更新w和b;
- 重复上述过程。
一般情况下,对于同一组训练数据,利用不同的神经网络训练之后,求其输出的平均值可以减少overfitting。Dropout就是利用这个原理,每次丢掉一半的一隐藏层神经元,相当于在不同的神经网络上进行训练,这样就减少了神经元之间的依赖性,即每个神经元不能依赖于某几个其他的神经元(指层与层之间相连接的神经元),使神经网络更加能学习到与其他神经元之间的更加健壮robust的特征。
07-3 深度学习RNN
RNN是一类扩展的人工神经网络,它是为了对序列数据进行建模而产生的。
针对对象:序列数据。例如文本,是字母和词汇的序列;语音,是音节的序列;视频,是图像的序列;气象观测数据,股票交易数据等等,也都是序列数据。
核心思想:样本间存在顺序关系,每个样本和它之前的样本存在关联。通过神经网络在时序上的展开,我们能够找到样本之间的序列相关性 。
07-4 集成学习
基本思想
在机器学习中,直接建立一个高性能的分类器是很困难的。
但是,如果能找到一系列性能较差的分类器(弱分类器),并把它们集成起来的话,也许就能得到更好的分类器。
集成学习:使用一系列学习器进行学习,并使用某种规则把各个学习结果进行整合从而获得比单个学习器更好的学习效果的一种机器学习方法。
- 如果把单个分类器比作一个决策者的话,集成学习的方法就相当于多个决策者共同进行一项决策。
学习方法
Boosting:个体学习器间存在强依赖关系,必须串行生成的序列化方法;串行:下一个分类器只在前一个分类器预测不够准的实例上进行训练或检验。
Bagging:个体学习器间不存在强依赖关系,可同时生成的并行化方法。并行:所有的弱分类器都给出各自的预测结果,通过组合把这些预测结果转化为最终结果。
07-5 强化学习
智能体(Agent)
- 感知外界环境的状态(State)和奖励反馈(Reward),并进行学习和决策。智能体的决策功能是指根据外界环境的状态来做出不同的动作(Action),而学习功能是指根据外界环境的奖励来调整策略。
环境(Environment)
- 智能体外部的所有事物,并受智能体动作的影响而改变其状态,并反馈给智能体相应的奖励。
强化学习中的基本要素
- 环境的状态集合:S;
- 智能体的动作集合:A;
- 状态转移概率:p(s’|s,a),即智能体根据当前状态s做出一个动作a之后,下一个时刻环境处于不同状态s’的概率;
- 即时奖励:R : S × A × S’ → R,即智能体根据当前状态做出一个动作之后,环境会反馈给智能体一个奖励,这个奖励和动作之后下一个时刻的状态有关。